Vågor på djupt vatten
En speciell lösning av Laplaces ekvation som beskriver vågrörelse på en sjö eller havets yta är
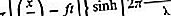
I detta fall är x-axeln utbredningsriktningen och z-axeln är vertikal; z = 0 beskriver den fria ytan på vattnet när det är ostört och z = −D beskriver bottenytan; ϕ 0 är en godtycklig konstant som bestämmer rörelsens amplitud; och f är vågens frekvens och λ deras våglängd. Om λ är mer än några centimeter är ytspänningen irrelevant och trycket i vätskan precis under dess fria yta är atmosfäriskt för alla värden på x. Det kan visas att vågrörelsen som beskrivs av (161) under dessa omständigheter endast överensstämmer med (157) om frekvensen och våglängden är relaterade till ekvationen

och ett uttryck för vågens hastighet kan härledas från detta, eftersom V = fλ. För grunt vatten (D << λ) får man svaret som redan citerats som ekvation (138), men för djupt vatten (D >> λ) är svaret
Vågor på djupt vatten är uppenbarligen spridande, och surfare litar på detta faktum. En storm mitt i havet stör ytan på ett kaotiskt sätt som skulle vara värdelöst för surfing, men när komponentvågorna rör sig mot stranden skiljs de åt; de med långa våglängder rör sig framför de med korta våglängder eftersom de reser snabbare. Som ett resultat verkar vågorna snyggt regelbundna när de anländer.
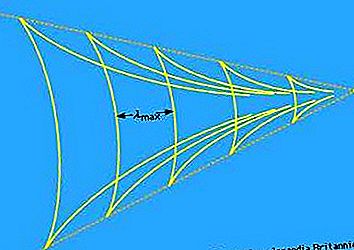
Alla som har observerat vågorna bakom ett rörligt fartyg vet att de är begränsade till ett V-format område på vattenytan, med fartyget vid spetsen. Vågorna är särskilt framträdande på armarna på V, men de kan också urskiljas mellan dessa armar där vågkammarna kurva på det sätt som anges i figur 12. Det verkar vara allmänt trott att V-vinkeln blir mer akut som båten snabbar upp, mycket på det sätt som den koniska chockvågen som följer med en supersonisk projektil blir mer akut (se figur 8). Så är inte fallet; den dispersiva karaktären av vågor på djupt vatten är sådan att V har en fast vinkel av två synd -1 (ett / tre) = 39 °. Thomson (Lord Kelvin) var den första som förklarade detta, och det V-formade området kallas nu Kelvin-kilen.
En version av Thomsons argument illustreras av diagrammet i figur 13. Här representerar S ("källan") fartygets båge som rör sig från vänster till höger med enhetlig hastighet U och linjerna märkta C, C ′, C ″ Etc. representerar en uppsättning parallella vågkammar som också rör sig från vänster till höger. Det kan visas att S kommer att skapa denna uppsättning av vapen om, men bara om den rider kontinuerligt på den som är märkt C. (Det kan också visas att även om vapnen i uppsättningen fortsätter på obestämd tid till vänster om C, där kan vara ingen till höger för den här.) Villkoret att S och C rör sig tillsammans indikerar att det finns ett samband mellan våglängden λ och lutningen α uttryckt av ekvationen

Detta villkor kan uppenbarligen uppfyllas av många andra uppsättningar av vapen förutom det som representeras av hela linjer i figuren - t.ex. av uppsättningen med något kortare våglängd λ ′ som representeras av trasiga linjer. När man tar hänsyn till alla uppsättningar som tillfredsställer (164) och som har våglängder mellan mellan λ och λ ′, blir det uppenbart att de över det mesta av området bakom källan stör störande. De förstärker varandra emellertid nära korsningarna som ringer i figuren. Dessa korsningar ligger på en linje genom S med lutning ß, där
Det följer att, även om vinkeln α kan ta vilket som helst värde mellan 90 ° (motsvarande λ = λ max = 2πU 2 / g) och noll, kan tan β aldrig överstiga ett / två Kvadratrot of√2, och synd β kan aldrig överstiga ett / tre.
Fartyg förlorar energi till vågorna i Kelvin-kilen, och de upplever ytterligare motstånd för det. Motståndet är särskilt högt när vågsystemet som skapas av bågen, där vattnet skjuts åt sidan, förstärker det vågsystem som skapats av "antikällan" vid aktern, där vattnet stängs igen. Sådan förstärkning kan komma att inträffa när den effektiva längden på båten, L, är lika med (2n + 1) λ max / 2 (med n = 0, 1, 2, …) och därför när Froude-numret, U / Kvadratrot av √ (Lg), tar ett av värdena [Kvadratrot av √ (2n + 1) π] −1. När en båt emellertid har påskyndats förbi U = kvadratrot av √ (Lg / π) tenderar dock bågen och aktervågorna att avbrytas, och motståndet till följd av vågskapande minskar.
Vågor på djupt vatten vars våglängd är några centimeter eller mindre benämns i allmänhet krusningar. I sådana vågor är tryckskillnaderna över den krökta ytan på vattnet associerat med ytspänning (se ekvation [129]) inte försumbar, och det lämpliga uttrycket för deras utbredningshastighet är

Våghastigheten är därför stor för mycket korta våglängder såväl som för mycket långa. För vatten vid normala temperaturer har V ett minimivärde av cirka 0,23 meter per sekund där våglängden är ungefär 17 millimeter, och det följer (notera att ekvation [164] inte har någon verklig rot för α såvida U inte överstiger V) att ett föremål rör sig genom vatten kan det inte skapa några krusningar alls om dess hastighet överstiger 0,23 meter per sekund. En vind som rör sig över vattenytan skapar inte heller krusningar om dess hastighet överstiger ett visst kritiskt värde, men detta är ett mer komplicerat fenomen och den kritiska hastigheten i fråga är tydligt högre.