Riemann-hypotesen, i talteori, hypotesen av den tyska matematikern Bernhard Riemann angående placeringen av lösningar på Riemann zeta-funktionen, som är kopplad till primtalssatsen och har viktiga konsekvenser för fördelningen av primtal. Riemann inkluderade hypotesen i ett papper, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" ("På antalet främsta siffror mindre än en given mängd"), publicerad i november 1859-utgåvan av Monatsberichte der Berliner Akademie ("Månadsöversikt" av Berlin Academy ”).
Zeta-funktionen definieras som den oändliga serien ζ (s) = 1 + 2 −s + 3 −s + 4 −s + ⋯, eller, i mer kompakt notation, , där summeringen (Σ) av termer för n går från 1 till oändlighet genom de positiva heltal och s är ett fast positivt heltal större än 1. Zeta-funktionen studerades först av den schweiziska matematikern Leonhard Euler på 1700-talet. (Av denna anledning kallas den ibland Euler zeta-funktionen. För ζ (1) är denna serie helt enkelt den harmoniska serien, känd sedan antiken att öka utan bunden - dvs. summan är oändlig.) Euler uppnådde omedelbar berömmelse när han bevisat i 1735 att ζ (2) = π 2 /6, ett problem som hade undgått de största matematiker av eran, inklusive den schweiziska Bernoulli familjen (Jakob, Johann, och Daniel). Mer generellt upptäckte Euler (1739) ett samband mellan värdet på zeta-funktionen för jämna heltal och Bernoulli-siffrorna, som är koefficienterna i utvidgningen av Taylor-serien av x / (e x - 1). (Se även exponentiell funktion.) Ännu mer häpnadsväckande upptäckte Euler 1737 en formel som hänför sig till zeta-funktionen, som innebär att summera en oändlig sekvens av termer som innehåller positiva heltal, och en oändlig produkt som involverar varje primtal:
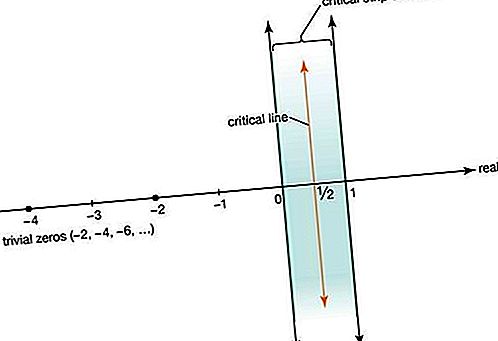
Riemann utökade studien av zeta-funktionen till att inkludera komplexa siffrorna x + iy, där i = kvadratrot av √ − 1, med undantag för linjen x = 1 i det komplexa planet. Riemann visste att zeta-funktionen är lika med noll för alla negativa jämna heltal −2, −4, −6,
(så kallade triviala nollor) och att den har ett oändligt antal nollor i den kritiska remsan med komplexa siffror som strikt faller mellan linjerna x = 0 och x = 1. Han visste också att alla icke-nollrivna nollor är symmetriska med avseende på kritiska linjen x = ett / 2. Riemann antog att alla nontriviala nollor är på den kritiska linjen, en antagning som senare blev känd som Riemann-hypotesen.
I 1914 engelska matematiker Godfrey Harold Hardy visat att ett oändligt antal lösningar av ζ (s) = 0 existera på den kritiska linjen x = ett / två. Därefter visades det av olika matematiker att en stor del av lösningarna måste ligga på den kritiska linjen, även om de ofta "bevisen" för att alla de icke-privata lösningarna finns på det har varit felaktiga. Datorer har också använts för att testa lösningar, med de första 10 biljoner nontriviala lösningarna som visas på den kritiska linjen.
Ett bevis på Riemann-hypotesen skulle få långtgående konsekvenser för talteorin och för användning av primer i kryptografi.
Riemann-hypotesen har länge betraktats som det största olösta problemet i matematik. Det var ett av 10 olösta matematiska problem (23 i den tryckta adressen) som presenterades som en utmaning för 1900-talets matematiker av den tyska matematikern David Hilbert vid den andra internationella matematik Kongressen i Paris den 8 augusti 1900. År 2000 amerikansk matematiker Stephen Smale uppdaterade Hilberts idé med en lista över viktiga problem för 2000-talet; Riemann-hypotesen var nummer ett. År 2000 utsågs det till ett Millennium Problem, ett av sju matematiska problem som valts ut av Clay Mathematics Institute i Cambridge, Mass., USA, för en särskild utmärkelsen. Lösningen för varje Millennium Problem är värt 1 miljon dollar. 2008 listade US Defense Advanced Research Projects Agency (DARPA) det som en av DARPA matematiska utmaningar, 23 matematiska problem för vilka de begärde forskningsförslag för finansiering - ”Matematisk utmaning Nitten: Avrätta Riemann-hypotesen. Den heliga gralen för talteori. ”